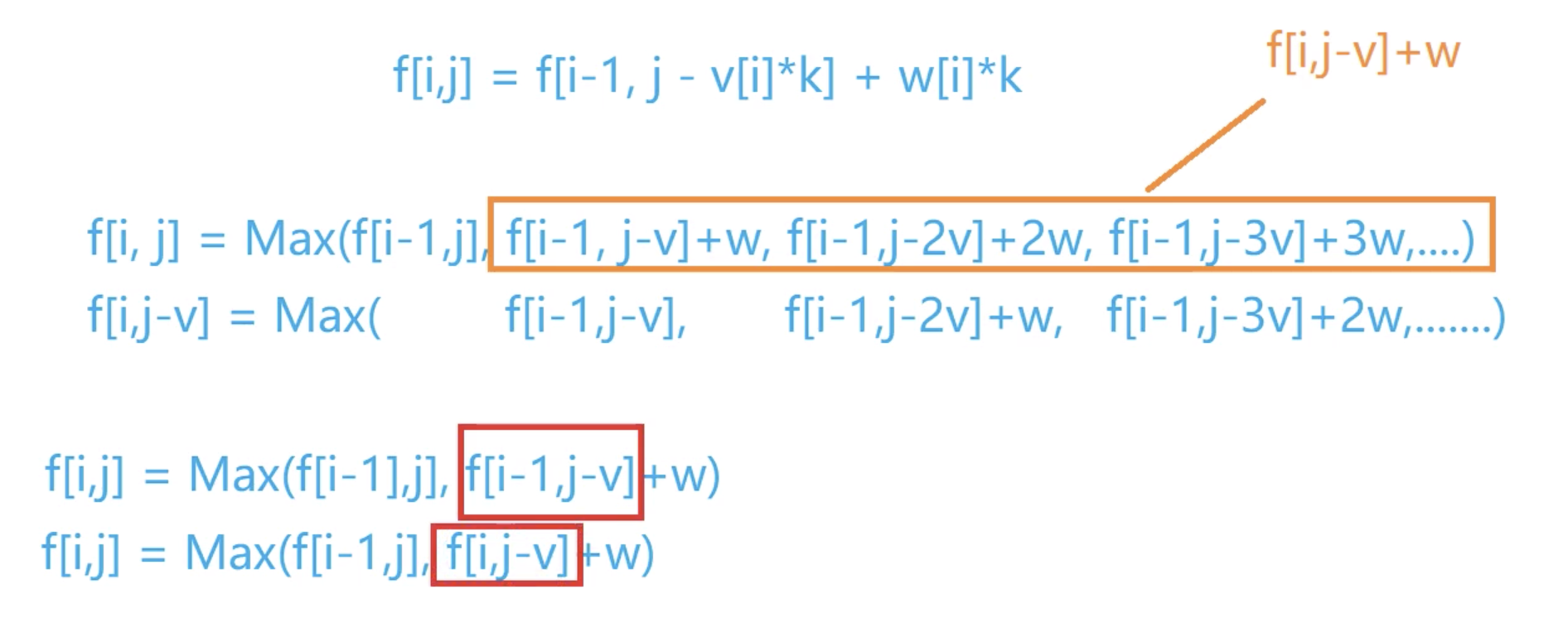DP 问题分析方法

DP 分析框架

背包问题

给一些物品，每件物品的体积是 $v_i$ ，价值是 $w_i$ ，有一个背包，体积是 V，问背包可以装下的物品的最大价值是多少？

01 背包

每件物品最多只能用一次

状态转移方程：

$f(i,j) = max(f(i-1, j), f(i-1, j-v_i) + w_i)$

$f(i, j)$ 表示在前 i 个物品中选择，且总体积不大于 j 的所有选法中的价值最大值。

01 背包问题

#include <iostream>
using namespace std;

const int N = 1010;
int n, m;
int w[N], v[N];
int f[N][N];

int main() {
    cin >> n >> m;
    for(int i=1;i<=n;i++) {
        cin >> v[i] >> w[i];
    }
    for(int i=1;i<=n;i++) {
        for(int j=0;j<=m;j++) {
            f[i][j] = f[i-1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i]);
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

滚动数组优化：

#include <iostream>
using namespace std;

const int N = 1010;

int v[N], w[N];
int n, m;
int f[N];

int main() {
    cin >> n >> m;
    for(int i=1;i<=n;i++) cin >> v[i] >> w[i];
    for(int i=1;i<=n;i++) {
        for(int j=m;j>=v[i];j--) {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
    cout << f[m] << endl;
    return 0;
}

完全背包

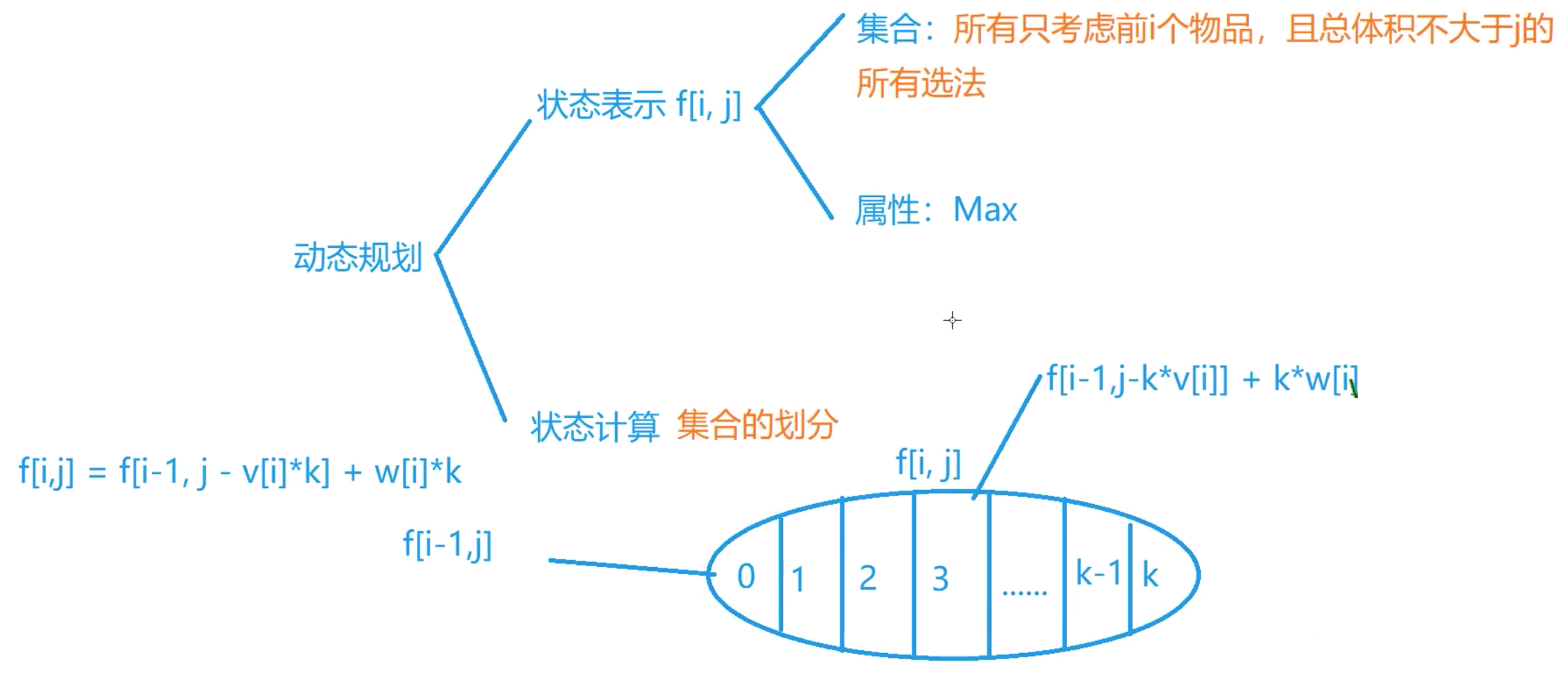
每件物品有无限个

完全背包 DP 分析

完全背包问题

朴素做法，直接实现状态转移方程 f[i][j] = f[i-1][j-k*v[i]] + k*w[i]，在 k*v[i] < j 的前提下让 k 取遍所有值。

#include <iostream>
using namespace std;

const int N = 1010;

int v[N], w[N];
int n, m;
int f[N][N];

int main() {
    cin >> n >> m;
    for(int i=1;i<=n;i++) cin >> v[i] >> w[i];
    for(int i=1;i<=n;i++) {
        for(int j=0;j<=m;j++) {
            for(int k=0; k*v[i]<=j; k++) {
                f[i][j] = max(f[i][j], f[i-1][j - k*v[i]] + k*w[i]);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

可以继续优化

$f(i, j) = max(f(i-1, j), f(i-1, j-v_i) + w_i, f(i-1,j-2v_i) + 2w_i, f(i-1,j-3v_i) + 3w_i, \dotso, f(i-1, j-sv_i) + s_iw_i)$ ，其中 $s=\lfloor j/v_i \rfloor$

$f(i, j-v_i) = max(f(i-1, j-v_i), f(i-1, j-2v_i) + w_i, f(i-1, j-3v_i) + 2w_i, \dotso), f(i-1, j-sv_i) + s_iw_i)$ ，其中 $s=\lfloor j/v_i \rfloor$

两式的最后一项是相等的，因为完全背包问题中每一类物品数量无限，s 最大能取到的数就是 $s=\lfloor j/v_i \rfloor$ ，因为必须 $j-sv_i \geq 0.$

对比两式可以得到：

$f(i,j) = max(f(i-1, j), f(i, j-v_i) + w_i)$

与 01 背包问题的状态转移方程非常类似：

$f(i,j) = max(f(i-1, j), f(i-1, j-v_i) + w_i)$

只相差 i-1 这里。

完全背包优化

#include <iostream>
using namespace std;

const int N = 1010;

int v[N], w[N];
int n, m;
int f[N][N];

int main() {
    cin >> n >> m;
    for(int i=1;i<=n;i++) cin >> v[i] >> w[i];
    for(int i=1;i<=n;i++) {
        for(int j=0;j<=m;j++) {
            f[i][j] = f[i-1][j];
            if(j>=v[i]) {
                f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

由于 f[i] 只用到了 f[i-1]，j - v[i] < j，计算 f[j] 时 f[j - v[i]] 一定已经被算出来了，可以继续进行滚动数组优化：

#include <iostream>
using namespace std;

const int N = 1010;

int v[N], w[N];
int n, m;
int f[N];

int main() {
    cin >> n >> m;
    for(int i=1;i<=n;i++) cin >> v[i] >> w[i];
    for(int i=1;i<=n;i++) {
        for(int j=v[i];j<=m;j++) {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
    cout << f[m] << endl;
    return 0;
}

多重背包

每件物品的价值为 $w_i$ ，体积为 $v_i$ ，个数有 $s_i$ 个。

朴素版本：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N], s[N];
int f[N][N];

int main() {
    cin >> n >> m;
    for(int i=1; i<=n; i++) cin >> v[i] >> w[i] >> s[i];
    
    for(int i=1;i<=n;i++) {
        for(int j=0;j<=m;j++) {
            // 依次考虑第 i 件物品选择多少个，从 0 一直枚举到 s[i]
            for(int k=0; k<=s[i] && k*v[i] <=j; k++) {
                f[i][j] = max(f[i][j], f[i-1][j-v[i]*k]+w[i]*k);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

多重背包问题可以使用二进制优化。思想是，对于每种物品的可选个数，不再从 0 到 $s_i$ 暴力枚举，将每种物品分成若干组，每组物品的个数为 $1, 2, 4, \dotso , 2^k, c$ ，总和为 $s_i$ ， $c < 2^{k+1}$ 。可以证明通过整组地选择物品，能够凑出 $0 \sim s_i$ 个物品。

证明思路：选择第一组，可以凑出 0 ~ 1 个物品，在此基础上考虑加上第二组，能够凑出 2 ~ 3 个物品，由于第一组可以凑出 0 ~ 1 个物品，所以前两组能够凑出 0 ~ 3 个物品。以此类推，一直到 $2^k$ 可以凑出 $0 \sim 2^{k+1} - 1$ 个物品，加上 c 之后，可以凑出 $c \sim 2^{k+1} - 1 + c$ 个物品，由于 $c < 2^{k+1}$ ，在 $2^{k+1} - 1$ 与 c 之间没有空隙。所以一共可以凑出 $0 \sim 2^{k+1} - 1 + c$ 也就是 $0 \sim s_i$ 个物品。

二进制优化版本：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 25000, M = 2010;

int n, m;
int v[N], w[N];
int f[N];

int main() {
    cin >> n >> m;
    // 每组物品的编号
    int cnt = 0;

    for(int i=1; i<=n; i++) {
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while(k<=s) {
            cnt++;
            // 第 cnt 个物品，体积为当前物品的体积乘以这堆物品的个数
            v[cnt] = a * k;
            // 价值为当前物品的价值乘以这堆物品的个数
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if(s > 0) {
            cnt ++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    n = cnt;
    // 直接套用 0-1 背包
    for(int i=1;i<=n;i++) {
        for(int j=m; j>=v[i]; j--) {
            f[j] = max(f[j], f[j-v[i]] + w[i]);
        }
    }
    cout << f[m] << endl;
    return 0;
}

另一种写法：

#include <iostream>
using namespace std;

const int N = 2010;

int f[N];

int n, m;

int main() {
  cin >> n >> m;
  for (int i = 0; i < n; i++) {
    int v, w, s;
    cin >> v >> w >> s;
    // 把每种物品拆分成 1 份、2 份、4 份... 分组打包
    for (int k = 1; k <= s; k *= 2) {
      for (int j = m; j >= k * v; j--) {
        f[j] = max(f[j], f[j - k * v] + k * w);
      }
      s -= k;
    }
    // 处理最后一包物品
    if (s) {
      for (int j = m; j >= s * v; j--) {
        f[j] = max(f[j], f[j - s * v] + s * w);
      }
    }
  }
  cout << f[m] << endl;
  return 0;
}

分组背包

有 N 组物品和一个容量是 V 的背包。

每组物品有若干个，同一组内的物品最多只能选一个。

每件物品的体积是 $v_{ij}$ ，价值是 $w_{ij}$ ，其中 i 是组号，j 是组内编号。

#include <iostream>
using namespace std;

const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N];
int f[N];

int main() {
    cin >> n >> m;
    for(int i=1;i<=n;i++) {
        cin >> s[i];
        for(int j=0;j<s[i];j++) {
            cin >> v[i][j] >> w[i][j];
        }
    }
    for(int i=1;i<=n;i++) {
        for(int j=m;j>=0;j--) {
            for(int k=0;k<s[i];k++) {
                if(v[i][k] <= j) {
                    f[j] = max(f[j], f[j-v[i][k]] + w[i][k]);
                }
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}