线性 DP

递推方程是有线性关系的。时间复杂度为状态数量乘以状态转移的计算量。

数字三角形

原题链接

如果下标涉及到 f[i-1]，i 一般从 1 开始枚举，设定 f[0] 为边界值，避免一些 if 判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
using namespace std;

const int N = 510, INF = 1e9;
int n;

int a[N][N], f[N][N];

int main() {
  cin >> n;
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= i; j++) {
      cin >> a[i][j];
    }
  }
  // 计算每行第一个数时，左上方的数不存在；计算每行最后一个数时，右上方的数不存在。都要初始化为负无穷。
  for (int i = 0; i <= n; i++) {
    for (int j = 0; j <= i + 1; j++) {
      f[i][j] = -INF;
    }
  }
  f[1][1] = a[1][1];
  int res = -INF;
  for (int i = 2; i <= n; i++) {
    for (int j = 1; j <= i; j++) {
      f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
    }
  }
  for (int i = 1; i <= n; i++) {
    res = max(res, f[n][i]);
  }
  cout << res << endl;
  return 0;
}

最长上升子序列

原题链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
using namespace std;

const int N = 1010;
int n;
int a[N], f[N];

int main() {
  cin >> n;
  for (int i = 1; i <= n; i++) cin >> a[i];
  for (int i = 1; i <= n; i++) {
    f[i] = 1;
    for (int j = 1; j < i; j++) {
      if (a[j] < a[i]) {
        f[i] = max(f[i], f[j] + 1);
      }
    }
  }
  int res = 0;
  for (int i = 1; i <= n; i++) res = max(res, f[i]);
  cout << res << endl;
  return 0;
}

求具体方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
using namespace std;

const int N = 1010;
int n;
int a[N], f[N], g[N];

int main() {
  scanf("%d", &n);
  for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
  for (int i = 1; i <= n; i++) {
    f[i] = 1;
    g[i] = 0;
    for (int j = 1; j < i; j++) {
      if (a[j] < a[i]) {
        if (f[i] < f[j] + 1) {
          f[i] = f[j] + 1;
          // 记录状态转移，以 a[i] 结尾的 LIS 的前一个数是 a[j]
          g[i] = j;
        }
      }
    }
  }
  // 循环结束后，k 是 LIS 中最后一个数的数组下标
  int k = 1;
  for (int i = 1; i <= n; i++) {
    if (f[k] < f[i]) {
      k = i;
    }
  }
  // LIS 的长度为 f[k]
  for (int i = 0, len = f[k]; i < len; i++) {
    printf("%d ", a[k]);
    // g[k] 表示第 k 个位置是从数组哪个位置位置转移过来的
    k = g[k];
  }
  return 0;
}

最长上升子序列 2

原题链接

本题的数据量范围比较大，N 为十万，需要进行优化。

按照 LIS 的长度进行分类，q[i] 表示长度为 i 的 LIS 中结尾元素数值的最小值。q[0] 为哨兵，值设置为负无穷。

q 数组显然单调递增，例如长度为 4 的 LIS 中的最后一个元素的最小值一定比长度为 3 的 LIS 中的最后一个元素的最小值要大。

反证法：假设长度为 4 的 LIS 中的最后一个元素的最小值等于长度为 3 的 LIS 中的最后一个元素的最小值。在长度为 4 的 LIS 中倒数第二个数一定比最后一个元素小，也就是找到了一个长度为 3 的 LIS 最后一个元素的值要小于假设中的长度为 3 的 LIS 中的最后一个元素的最小值，发生矛盾。

在 q 数组中找到一个最大的小于 a[i] 的数，假设为 q[k]，然后把 a[i] 接到他的后面，就构成了长度为 k + 1 的 LIS。q 数组单调递增，因此在 q 数组中寻找一个最大的小于 a[i] 的数可以用二分来做。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int q[N];
int n;
int main() {
  scanf("%d", &n);
  for (int i = 0; i < n; i++) scanf("%d", &a[i]);
  int len = 0;
  q[0] = -2e9;
  for (int i = 0; i < n; i++) {
    int l = 0, r = len;
    while (l < r) {
      int mid = l + r + 1 >> 1;
      if (q[mid] < a[i])
        l = mid;
      else
        r = mid - 1;
    }
    len = max(len, r + 1);
    q[r + 1] = a[i];
  }
  printf("%d\n", len);
  return 0;
}

最长公共子序列

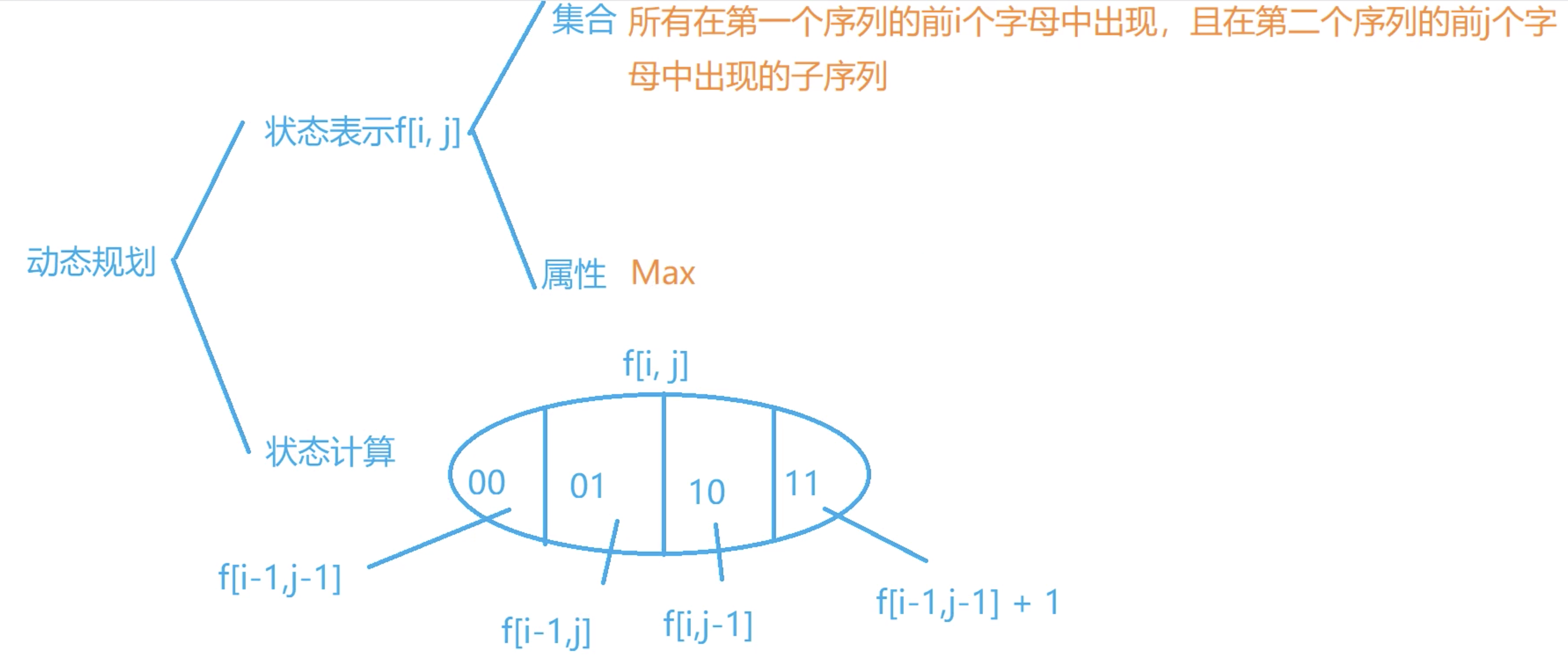
最长公共子序列 DP 分析

f[i][j] 表示的集合为：所有在第一个序列的前 i 个字母中出现，且在第二个序列的前 j 个字母中出现的子序列。

属性为：子序列长度的最大值。

集合划分方式：a[i]，b[j] 是否包含在子序列当中为划分依据。

共有四种情况：

  1. 不选 a[i] 不选 b[j]。
  2. 不选 a[i] 选 b[j]。
  3. 选 a[i] 不选 b[j]。
  4. 选 a[i] 选 b[j]。

第一种情况 f[i][j] = f[i-1][j-1]。
第四种情况 f[i][j] = f[i-1][j-1] + 1。

第二种情况 f[i][j] = f[i-1][j]。
第三种情况 f[i][j] = f[i][j-1]。

需要注意的是，f[i-1][j] 表示的集合并不是第二种情况。根据集合定义，f[i-1][j] 表示所有在第一个序列的前 i-1 个字母中出现，且在第二个序列的前 j 个字母中出现的子序列长度的最大值。这个最大值取到的时候，子序列不一定包含 b[j] 这个数。因为我们最终要求最大值，f[i-1][j] 表示的集合能覆盖第二种情况，用这个最大值来代替第二种情况的最大值是没有问题的。

第一种情况 f[i-1][j-1] 被第二种和第三种情况的集合覆盖，所以不用单独考虑，f[i-1][j] 和 f[i][j-1] 的最大值能够包含 1、2、3 三种情况。

这样的划分是有重叠的，但不影响，因为全局最大值等于所有集合划分的最大值。即使这些集合有重叠也无所谓。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main() {
  cin >> n >> m;
  cin >> a + 1 >> b + 1;

  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
      f[i][j] = max(f[i - 1][j], f[i][j - 1]);
      if (a[i] == b[j]) {
        f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
      }
    }
  }
  cout << f[n][m] << endl;
  return 0;
}

最短编辑距离

原题链接

编辑距离 DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
using namespace std;

int n, m;
const int N = 1010;
char a[N], b[N];
int f[N][N];

int main() {
  scanf("%d%s", &n, a + 1);
  scanf("%d%s", &m, b + 1);
  for (int i = 0; i <= n; i++) f[i][0] = i;
  for (int i = 0; i <= m; i++) f[0][i] = i;
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
      f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
      if (a[i] == b[j])
        f[i][j] = min(f[i][j], f[i - 1][j - 1]);
      else
        f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
    }
  }
  printf("%d\n", f[n][m]);
  return 0;
}

编辑距离

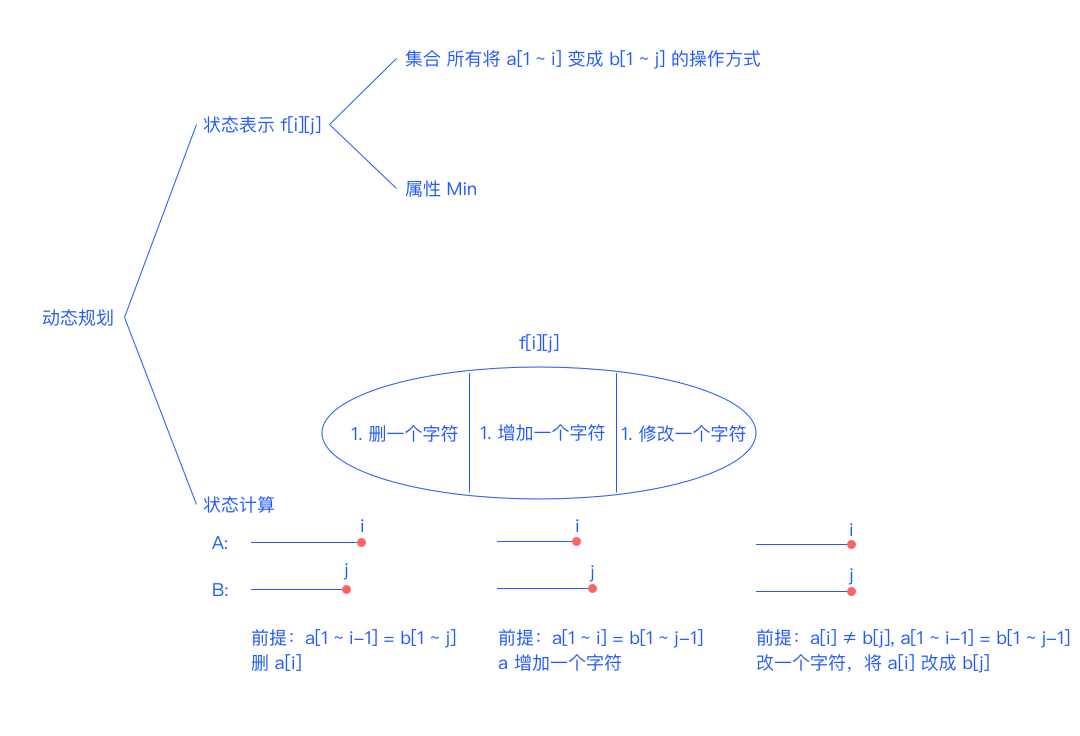
编辑距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <string.h>

#include <algorithm>
#include <iostream>
using namespace std;

const int N = 15, M = 1010;

int n, m;
int f[N][N];
char str[M][N];
int edit_distance(char a[], char b[]) {
  int la = strlen(a + 1);
  int lb = strlen(b + 1);
  for (int i = 0; i <= la; i++) f[i][0] = i;
  for (int i = 0; i <= lb; i++) f[0][i] = i;
  for (int i = 1; i <= la; i++) {
    for (int j = 1; j <= lb; j++) {
      f[i][j] = min(f[i][j - 1] + 1, f[i - 1][j] + 1);
      f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j]));
    }
  }
  return f[la][lb];
}
int main() {
  scanf("%d%d", &n, &m);
  for (int i = 0; i < n; i++) scanf("%s", str[i] + 1);
  while (m--) {
    char s[N];
    int limit;
    scanf("%s%d", s + 1, &limit);
    int res = 0;
    for (int i = 0; i < n; i++) {
      if (edit_distance(str[i], s) <= limit) res++;
    }
    printf("%d\n", res);
  }
}

区间 DP

石子合并

原题链接

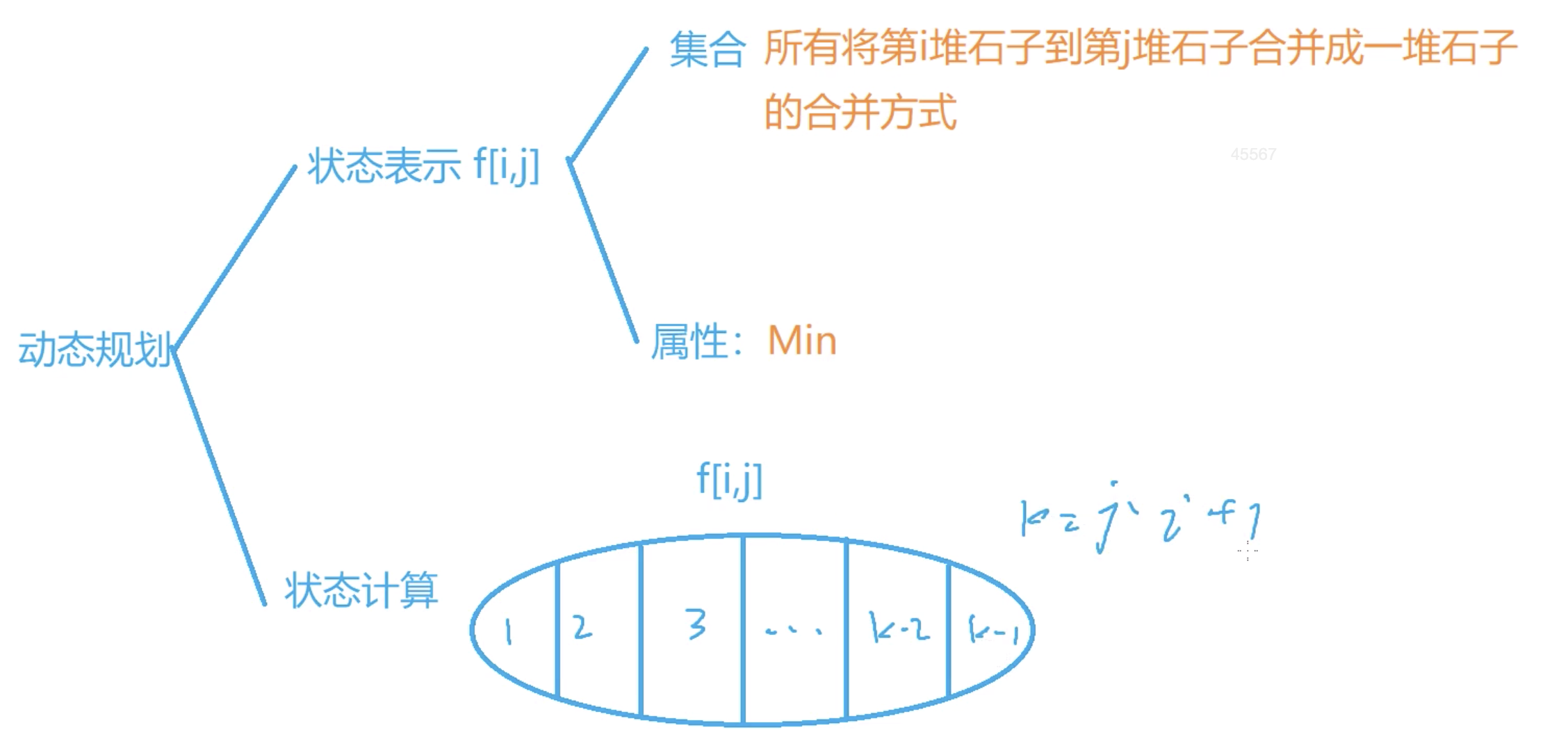
石子合并 DP 分析

集合表示：f[i][j] 表示所有将第 i 堆到第 j 堆石子合并成一堆石子的合并方式。
属性：代价最小值。
集合划分依据：最后一次合并的分界线。
状态转移方程：f[i][j] = min(f[i][k] + f[k+1][j] + s[j] - s[i-1]), i <= k <= j - 1

解释：考虑第 i 堆到第 j 堆石子，最后一次合并是发生在哪个位置。从 i 到 j 之间枚举这个分界点的位置 k。计算将第 i 堆到第 k 堆石子合并成一堆石子的合并代价最小值，计算将第 k+1 堆到第 j 堆石子合并成一堆石子的合并代价最小值，最后还要加上将 i~k 与 k+1~j 这两堆石子合并的代价，也就是 ∑k=ijak\sum\limits_{k=i}^{j}a_k。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
using namespace std;

const int N = 310;

int n;
int s[N];
int f[N][N];

int main() {
  cin >> n;
  for (int i = 1; i <= n; i++) cin >> s[i];
  // 计算前缀和，便于快速计算任意区间内的和
  for (int i = 1; i <= n; i++) s[i] += s[i - 1];
  // 枚举区间长度，区间长度 1 不用考虑，代价都是 0
  for (int len = 2; len <= n; len++) {
    for (int i = 1; i + len - 1 <= n; i++) {
      int l = i, r = i + len - 1;
      f[l][r] = 1e8;
      for (int k = l; k < r; k++) {
        f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
      }
    }
  }
  cout << f[1][n] << endl;
  return 0;
}

计数类 DP

整数划分

原题链接

可以转化为一个完全背包问题：有一个容量为 n 的背包，和 n 个物品，物品的体积分别为为 1, 2, ..., n，每个物品可以选无限次，求将背包装满的方案数量是多少。

f[i][j] 表示从 1 ~ i 中选，体积为 j 的所有选法的数量。

集合划分：第 i 个物品选择几个作为划分依据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
using namespace std;

const int N = 1010, mod = 1e9 + 7;

int n;
int f[N];

int main() {
  cin >> n;
  f[0] = 1;
  for (int i = 1; i <= n; i++) {
    for (int j = i; j <= n; j++) {
      f[j] = (f[j] + f[j - i]) % mod;
    }
  }
  cout << f[n] << endl;
  return 0;
}

另一种思路

整数划分 DP 分析

将集合划分成两类：

  1. 方案中包含 1。
  2. 方案中不包含 1。

第一类方案，将其中的 1 删掉，总和为 i-1，元素数量为 j-1，因此可以从 f[i-1][j-1] 转移到 f[i][j]。

第二类方案，将每一项减去 1，总和减去了 j * 1，元素个数仍为 j，因此可以从 f[i-j][j] 转移到 f[i][j]。

划分方案的总数需要将两类方案的数目相加。最终结果需要考虑总和是 n，可以表示成 1, 2, 3, ..., n 个数相加的所有方案，需要对 f[n][i] 进行累加。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
using namespace std;

const int N = 1010, mod = 1e9 + 7;
int n;
int f[N][N];

int main() {
  cin >> n;
  f[0][0] = 1;
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= i; j++) {
      f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;
    }
  }
  int res = 0;
  for (int i = 1; i <= n; i++) res = (res + f[n][i]) % mod;
  cout << res << endl;
  return 0;
}