最短路

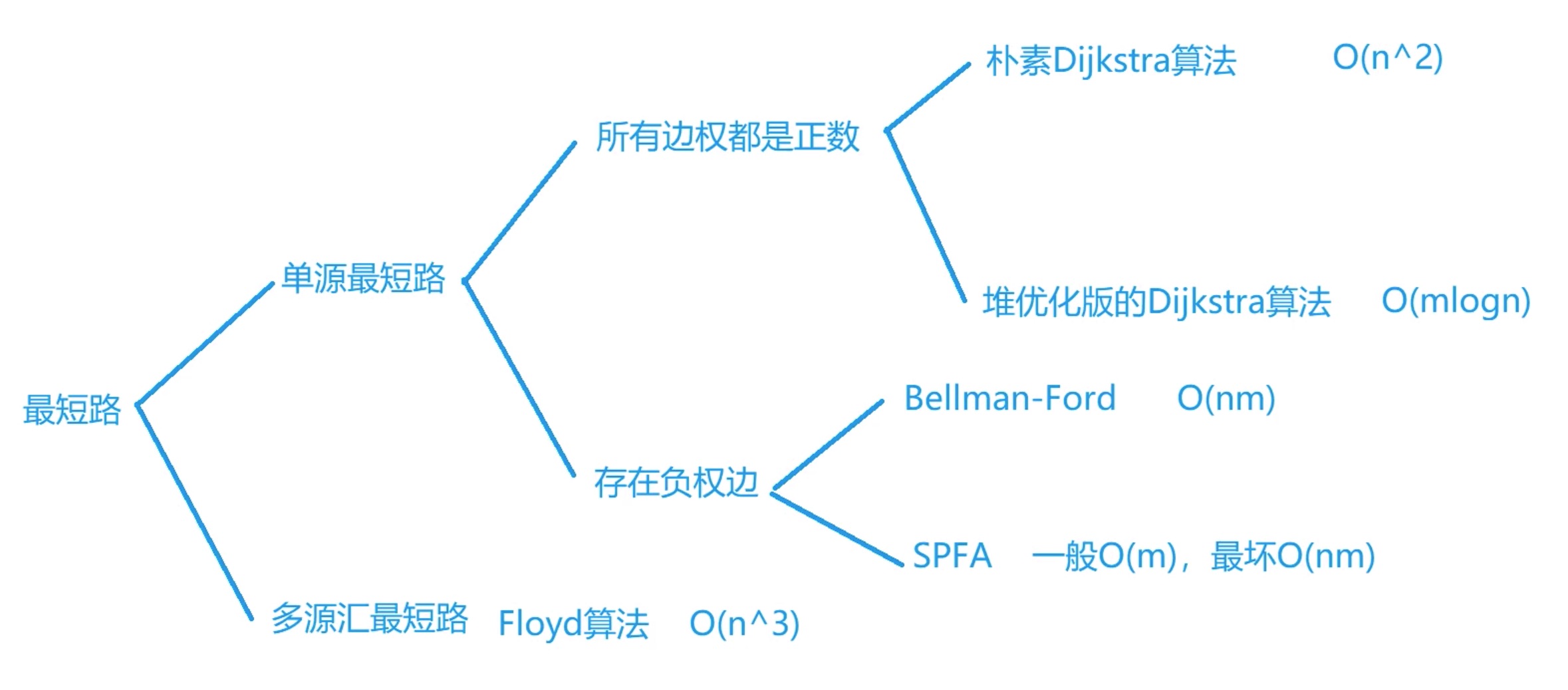
难点在建图，如何把问题抽象成一个图，转化成最短路问题。

最短路问题

单源最短路

所有边权都是正数

朴素 Dijkstra 算法

n 为节点数。

时间复杂度：O(n2)O(n^{2})

适合稠密图。即 m 与 n2n^{2} 是一个级别的，图中边比较多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <cstring>
using namespace std;

const int N = 510;
int g[N][N];
int d[N];
bool st[N];
int n, m;

int dijkstra() {
  d[1] = 0;
  // 有 n 个节点，一共需要做 n 次
  for(int i=0;i<n;i++) {
    // 寻找未访问过的节点中，距离源点最近的点，t 存储的是找到的节点
    int t = -1;
    for(int j=1;j<=n;j++) {
      if(!st[j] && (t == -1 || d[j] < d[t])) {
        t = j;
      }
    }
    // 将找到的节点标记为访问过
    st[t] = true;
    // 尝试从 t 节点绕路，用 d[t] 更新其他与 t 相连且未访问过的节点到源点的距离
    for(int j=1; j<=n; j++) {
      d[j] = min(d[j], d[t] + g[t][j]);
    }
  }
  if(d[n] == 0x3f3f3f3f) return -1;
  return d[n];
}

int main() {
  memset(g, 0x3f, sizeof g);
  memset(d, 0x3f, sizeof d);
  scanf("%d%d", &n, &m);
  while(m--) {
    int a, b, c;
    scanf("%d%d%d", &a, &b, &c);
    g[a][b] = min(g[a][b], c);
  }
  int t = dijkstra();
  printf("%d\n", t);
  return 0;
}

堆优化 Dijkstra 算法

n 为节点数，m 为边数。

时间复杂度：O(m⋅log(n))O(m \cdot log(n))

适合稀疏图。即 m 与 n 是一个级别的。

用堆存储所有点到起点的距离。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;

const int N = 1e6 + 10;

// <距离, 节点>
typedef pair<int, int> PII;

// w[i] 存储两个节点之间边的权值
int h[N], e[N], w[N], ne[N], idx;
int n, m;
bool st[N];
int d[N];

void add(int a, int b, int c) {
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++;
}
int dijkstra() {
    d[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, 1});
    while(heap.size()) {
        auto t = heap.top();
        heap.pop();

        int ver = t.second, dist = t.first;
        if(st[ver]) continue;
        st[ver] = true;
        // 通过邻接表找到所有相邻节点
        for(int i=h[ver];i!=-1;i=ne[i]) {
            int j = e[i];
            // 只要当前节点距离源点距离加上当前节点距离邻居节点的距离之和小于邻居节点到源点的距离，就更新 d[j]，然后放入小根堆
            if(dist + w[i] < d[j]) {
                d[j] = dist + w[i];
                heap.push({d[j], j});
            }
        }
    }
    if(d[n] == 0x3f3f3f3f) return -1;
    return d[n];
}
int main() {
    // 邻接表初始化为空
    memset(h, -1, sizeof h);
    // 距离数组初始化为正无穷
    memset(d, 0x3f, sizeof h);
    scanf("%d%d", &n, &m);
    while(m--) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }
    int t = dijkstra();
    printf("%d\n", t);
    return 0;
}

存在负权边

Bellman-Ford 算法

时间复杂度：O(n⋅m)O(n \cdot m)

可以求不超过 k 条边的最短路。

基本框架

1
2
3
4
for n 次  - 迭代 k 次，就是求不超过 k 条边的最短路
  for 所有边 <a, b, w>
    // 看一下从节点 1 走到节点 a 再从节点 a 走到 b 是否比直接从节点 1 走到节点 b 的路径要短，如果短就更新 dist[b] 的值
    dist[b] = min(dist[b], dist[a] + w); // 松弛操作

运行完后可以保证：dist[b] <= dist[a] + w，叫做三角不等式。

有边数限制的最短路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <cstring>
using namespace std;

int n, m, k;
const int M = 10010, N = 510;
int d[N], backup[N];
struct Edge {
    int a, b, w;
}edges[M];

int bellman_ford() {
    memset(d, 0x3f, sizeof d);
    d[1] = 0;
    for(int i=0; i<k; i++) {
        // 创建一个备份
        memcpy(backup, d, sizeof d);
        for(int j=0;j<m;j++) {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            d[b] = min(d[b], backup[a] + w);
        }
    }
    if(d[n] > 0x3f3f3f3f / 2) return -1;
    return d[n];
}

int main() {
    scanf("%d%d%d", &n, &m, &k);
    for(int i=0;i<m;i++) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a,b,w};
    }
    int t = bellman_ford();
    if(t == -1) puts("impossible");
    else printf("%d\n", t);
    return 0;
}

SPFA 算法（Shortest Path Fast Algorithm）

对 Bellman-Ford 算法进行了优化。

不能有负权回路，否则会死循环。

时间复杂度一般情况下：O(m)O(m)

时间复杂度最坏情况下：O(n⋅m)O(n \cdot m)

spfa 求最短路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <iostream>
#include <queue>
#include <cstring>

using namespace std;

const int N = 1e5 + 10;
int h[N], e[N], w[N], ne[N], idx;
int n, m;
bool st[N];
int d[N];

void add(int a, int b, int c) {
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++;
}

int spfa() {
    // 初始时所有点距离初始化为正无穷，节点 1 到源点距离初始化为 0
    memset(d, 0x3f, sizeof d);
    d[1] = 0;
    queue<int> q;
    // 将节点 1 放入队列，标记节点 1 在队列中
    q.push(1);
    st[1] = true;
    while(q.size()) {
        auto t = q.front();
        q.pop();
        st[t] = false;
        // 寻找与出队的节点相连的所有点
        for(int i=h[t];i!=-1;i=ne[i]) {
            int j = e[i];
            // 如果从出队的节点绕路比直接走要近，就更新距离数组
            if(d[j] > d[t] + w[i]) {
                d[j] = d[t] + w[i];
                if(!st[j]) {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    if(d[n] == 0x3f3f3f3f) return -1;
    return d[n];
}
int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    while(m--) {
        int a, b, w;
        cin >> a >> b >> w;
        add(a, b, w);
    }
    int t = spfa();
    if(t == -1) cout << "impossible" << endl;
    else cout << t << endl;
    return 0;
}

Tips:

  1. Bellman_ford 算法里最后 return -1 的判断条件写的是 dist[n] > 0x3f3f3f3f / 2；而 SPFA 算法写的是 dist[n] == 0x3f3f3f3f。其原因在于 Bellman_ford 算法会遍历所有的边，因此不管是不是和源点连通的边它都会得到更新；但是 SPFA 算法不一样，它相当于采用了 BFS，因此遍历到的结点都是与源点连通的，因此如果你要求的 n 和源点不连通，它不会得到更新，还是保持 0x3f3f3f3f。
  2. 求负环一般使用 SPFA 算法，使用一个 cnt 数组记录每个节点到源点经过的边数，每更新一次 d[j]，cnt[j] 就加一。一旦某个 cnt[x] 到达 n，就说明存在负环。

多源汇最短路

源指的就是起点。
汇指的就是终点。

Floyd 算法

时间复杂度：O(n3)O(n^{3})

图不能有负权回路。

直接将邻接矩阵转换为最短路径矩阵。d[a][b] 表示从 a 节点到 b 节点的最短距离。

Floyd 求最短路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 200, INF=1e9;
int n,m,Q;
int d[N][N];
// 三重循环，k i j 都循环 n 次
void floyd() {
    for(int k=1;k<=n;k++) {
        for(int i=1;i<=n;i++) {
            for(int j=1;j<=n;j++) {
                // 直走近还是绕路近
                d[i][j] = min(d[i][j], d[i][k]+ d[k][j]);
            }
        }
    }
}
int main() {
    scanf("%d%d%d", &n, &m, &Q);
    for(int i=1;i<=n;i++) {
        for(int j=1;j<=n;j++) {
            if(i == j) d[i][j] = 0;
            else d[i][j] = INF;
        }
    }
    while(m--) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        d[a][b] = min(d[a][b], w);
    }
    floyd();
    while(Q--) {
        int a, b;
        scanf("%d%d", &a, &b);
        if(d[a][b] > INF / 2) puts("impossible");
        else
        printf("%d\n", d[a][b]);
    }
    return 0;
}