1015. 摘花生

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| #include <iostream>
using namespace std;
const int N = 110;
int f[N][N];
int a[N][N];
int main() {
int T;
int R, C;
cin >> T;
while (T--) {
cin >> R >> C;
for (int i = 1; i <= R; i++) {
for (int j = 1; j <= C; j++) {
cin >> a[i][j];
}
}
for (int i = 1; i <= R; i++) {
for (int j = 1; j <= C; j++) {
f[i][j] = max(f[i][j - 1], f[i - 1][j]) + a[i][j];
}
}
cout << f[R][C] << endl;
}
return 0;
}
|
1018. 最低通行费
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| #include <iostream>
using namespace std;
const int N = 110, INF = 1e9;
int f[N][N];
int a[N][N];
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cin >> a[i][j];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == 1 && j == 1)
f[i][j] = a[i][j];
else {
f[i][j] = INF;
if (i > 1) {
f[i][j] = min(f[i][j], f[i - 1][j] + a[i][j]);
}
if (j > 1) {
f[i][j] = min(f[i][j], f[i][j - 1] + a[i][j]);
}
}
}
}
cout << f[n][n] << endl;
return 0;
}
|
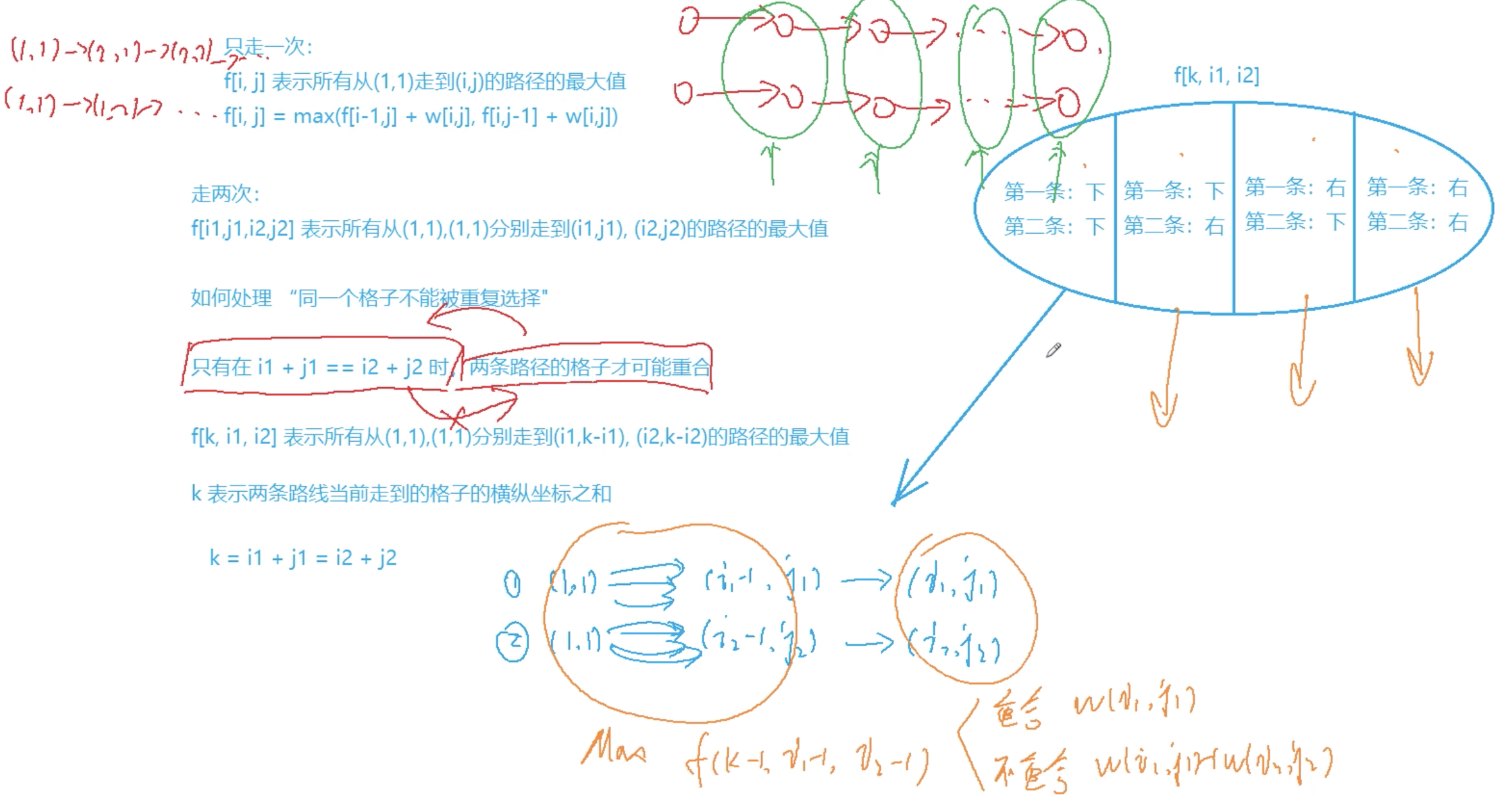
1027. 方格取数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <iostream>
using namespace std;
const int N = 15;
int n;
int f[2 * N][N][N];
int w[N][N];
int main() {
cin >> n;
int a, b, c;
while (cin >> a >> b >> c, a || b || c) {
w[a][b] = c;
}
for (int k = 2; k <= n + n; k++) {
for (int i1 = 1; i1 <= n; i1++) {
for (int i2 = 1; i2 <= n; i2++) {
int j1 = k - i1, j2 = k - i2;
if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n) {
int t = w[i1][j1];
if (i1 != i2) {
t += w[i2][j2];
}
int &x = f[k][i1][i2];
x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
x = max(x, f[k - 1][i1][i2 - 1] + t);
x = max(x, f[k - 1][i1 - 1][i2] + t);
x = max(x, f[k - 1][i1][i2] + t);
}
}
}
}
cout << f[n + n][n][n] << endl;
return 0;
}
|
275. 传纸条
这道题实际上和上面的代码一样,转化的过程比较 tricky。
证明
结论是没有交叉点的路线一定不会比有交点的路线差,用下面的算法虽然会计算那些不符合题意的相交的路线,但这样算出的结果一定不是最优的,在取 max 的时候会被淘汰。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <iostream>
using namespace std;
const int N = 55;
int f[2 * N][N][N];
int w[N][N];
int n, m;
int main() {
cin >> m >> n;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
cin >> w[i][j];
}
}
for (int k = 2; k <= n + m; k++) {
for (int i1 = 1; i1 <= m; i1++) {
for (int i2 = 1; i2 <= m; i2++) {
int j1 = k - i1, j2 = k - i2;
if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n) {
int t = w[i1][j1];
if (i1 != i2) {
t += w[i2][j2];
}
int &x = f[k][i1][i2];
x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
x = max(x, f[k - 1][i1][i2 - 1] + t);
x = max(x, f[k - 1][i1 - 1][i2] + t);
x = max(x, f[k - 1][i1][i2] + t);
}
}
}
}
cout << f[n + m][m][m] << endl;
return 0;
}
|



