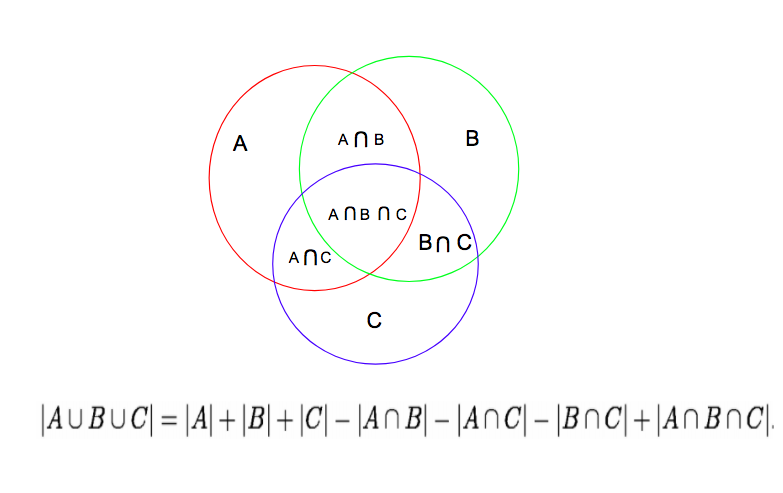容斥原理
可在离散数学(左孝凌)课本 p97 找到容斥原理的证明。容斥原理又叫包含排斥原理。
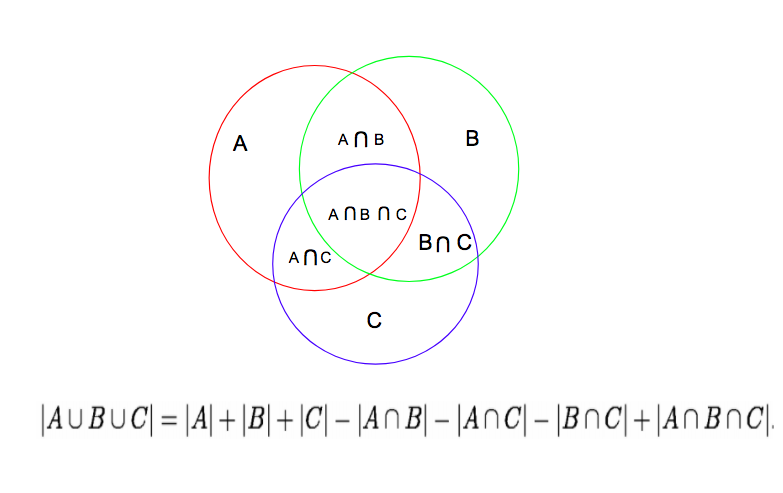
有三个集合时的公式如下:
∣S1∪S2∪S2∣=∣S1∣+∣S2∣+∣S3∣−∣S1∩S2∣−∣S1∩S3∣−∣S2∩S3∣+∣S1∩S2∩S3∣
组合恒等式:Cn0+Cn1+Cn2+⋯+Cnn=2n
容斥原理公式中一共有 2n−1 项,所以使用容斥原理计算一组集合的并集中元素个数的时间复杂度为 O(2n),n 为集合数量。
能被整除的数
枚举子集一般使用位运算。每一位代表选或不选一个元素。从 0 一直枚举到 2n−1 这些数字可以表示 n 个元素的子集的情况。本题不需要考虑一个都不选的情况,从 1 开始枚举。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <iostream>
using namespace std;
typedef long long LL;
int n, m;
int p[20];
int main() {
cin >> n >> m;
for(int i=0;i<m;i++) {
cin >> p[i];
}
int res = 0;
for(int i=1; i < 1 << m; i++) {
int t = 1, cnt = 0;
for(int j=0; j<m; j++) {
if(i >> j & 1) {
cnt ++;
if((LL)t * p[j] > n) {
t = -1;
break;
}
t *= p[j];
}
}
if(t!=-1) {
if(cnt % 2) res += n/t;
else res -= n/t;
}
}
cout << res << endl;
return 0;
}
|
Nim 游戏
给定 n 堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
假设有 n 堆石子,每堆石子有 ai 块石头。
如果 a1⊕a2⊕a3⊕⋯⊕an=0 那么先手必败。
如果 a1⊕a2⊕a3⊕⋯⊕an=0 那么先手必胜。
证明:
0⊕0⊕0⊕⋯⊕0=0
a1⊕a2⊕a3⊕⋯⊕an=x
设 x 的二进制表示中,最高位在第 k 位,那么 a1 an 中一定有 ai,其二进制表示中第 k 位的值为 1。
因为 ai⊕x<x,可以从 ai 中拿走 ai−(ai⊕x) 个石子,即将 ai 变成 (ai⊕x)。
a1⊕a2⊕a3⊕⋯⊕an
=a1⊕a2⊕a3⊕⋯⊕ai⊕x⊕ai+1⊕⋯⊕an
=x⊕x
=0
到此可以证明,如果 a1⊕a2⊕a3⊕⋯⊕an=0,一定存在一种操作方式,操作之后使 a1⊕a2⊕a3⊕⋯⊕an=0
接下来证明当 a1⊕a2⊕a3⊕⋯⊕an=0 时,无论如何操作,都会使得 a1⊕a2⊕a3⊕⋯⊕an=0
使用反证法,假设从 ai 中拿一些石子,使其变成 ai′,而 a1⊕a2⊕a3⊕⋯⊕ai′⊕ai+1⊕⋯⊕an=0
将两式上下进行异或
a1⊕a2⊕a3⊕⋯⊕ai′⊕ai+1⊕⋯⊕an=0
a1⊕a2⊕a3⊕⋯⊕ai⊕ai+1⊕⋯⊕an=0
可以得到:ai⊕ai′=0 即 ai=ai′,与题设矛盾。
Nim 游戏
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| #include <iostream>
using namespace std;
int main() {
int n;
scanf("%d", &n);
int res;
while(n--) {
int x;
scanf("%d", &x);
res ^= x;
}
if(res) puts("Yes");
else puts("No");
return 0;
}
|
Mex 运算
设 S 表示一个非负整数集合,定义 mex(S) 为求出不属于集合 S 的最小非负数整数的运算,即:mex(S) = { min(x) | x 属于自然数且 x 不属于 S }
SG 函数
在有向图游戏中,对于每个节点 x,设从 x 出发共有 k 条有向边,分别到达节点 y1, y2, …, yk,定义 SG(x) 为 x 的后继节点 y1, y2, …, yk 的 SG 函数值构成的集合再执行 mex(S) 运算的结果,即:SG(x) = mex({SG(y1), SG(y2), …, SG(yk)})
特别的,整个有向图游戏 G 的 SG 函数值被定义为有向图游戏起点 s 的 SG 函数值,即:SG(G) = SG(s)。
集合 - Nim 游戏
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| #include <iostream>
#include <unordered_set>
#include <cstring>
using namespace std;
const int N = 110, M = 10010;
int n, m;
int s[N], f[M];
int sg(int x) {
if(f[x] !=-1 ) return f[x];
unordered_set<int> S;
for(int i=0;i<m;i++) {
int sum = s[i];
if(x>=sum) S.insert(sg(x-sum));
}
for(int i=0; ;i++) {
if(!S.count(i)) {
return f[x] = i;
}
}
}
int main() {
cin >> m;
for(int i=0;i<m;i++) {
cin >> s[i];
}
cin >> n;
memset(f, -1, sizeof f);
int res = 0;
for(int i=0;i<n;i++) {
int x;
cin >> x;
res ^= sg(x);
}
if(res) puts("Yes");
else puts("No");
return 0;
}
|