1021. 货币系统

完全背包问题求方案数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>

using namespace std;

typedef long long LL;
const int N = 3010;
int n, m;
LL f[N];

int main() {
  cin >> n >> m;
  f[0] = 1;
  for (int i = 0; i < n; i++) {
    int v;
    cin >> v;
    for (int j = v; j <= m; j++) {
      f[j] += f[j - v];
    }
  }
  cout << f[m] << endl;
  return 0;
}

532. 货币系统

求极大线性无关组中的向量个数。完全背包问题。

  1. a1,a2,… ,ana_1, a_2, \dotso, a_n 一定都可以被表示出来。
  2. 最优解中，b1,b2,… ,bmb_1, b_2, \dotso, b_m 一定是从 a1,a2,… ,ana_1, a_2, \dotso, a_n 中选择的。
  3. b1,b2,… ,bmb_1, b_2, \dotso, b_m 一定不能被其他 bib_i 表示出来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 110, M = 25010;

int n;
int a[N];
int f[M]; // f[a[i]] 表示用 a[1 ~ i-1] 凑成 a[i] 的方案数

int main() {
  int T;
  cin >> T;
  while (T--) {
    cin >> n;
    for (int i = 0; i < n; i++) cin >> a[i];
    sort(a, a + n);
    int m = a[n - 1];
    memset(f, 0, sizeof f);
    f[0] = 1;

    int res = 0;
    for (int i = 0; i < n; i++) {
      if (!f[a[i]]) res++;
      for (int j = a[i]; j <= m; j++) {
        f[j] += f[j - a[i]];
      }
    }
    cout << res << endl;
  }
}

7. 混合背包问题

在状态计算的时候，根据物品种类来选用 01 背包、完全背包、多重背包的状态转移方程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
using namespace std;

const int N = 1010;
int n, m;
int f[N];

int main() {
  cin >> n >> m;
  for (int i = 0; i < n; i++) {
    int v, w, s;
    cin >> v >> w >> s;
    if (s == 0) {  // 完全背包
      for (int j = v; j <= m; j++) {
        f[j] = max(f[j], f[j - v] + w);
      }
    } else {
      if (s == -1) s = 1; // 01 背包可以看成特殊的多重背包
      // 多重背包二进制优化
      for (int k = 1; k <= s; k *= 2) {  // 处理第 1 包物品、第 2 包 ...
        for (int j = m; j >= k * v; j--) {
          f[j] = max(f[j], f[j - k * v] + k * w);
        }
        s -= k;
      }
      // 处理最后一包物品
      if (s) {
        for (int j = m; j >= s * v; j--) {
          f[j] = max(f[j], f[j - s * v] + s * w);
        }
      }
    }
  }
  cout << f[m] << endl;
  return 0;
}

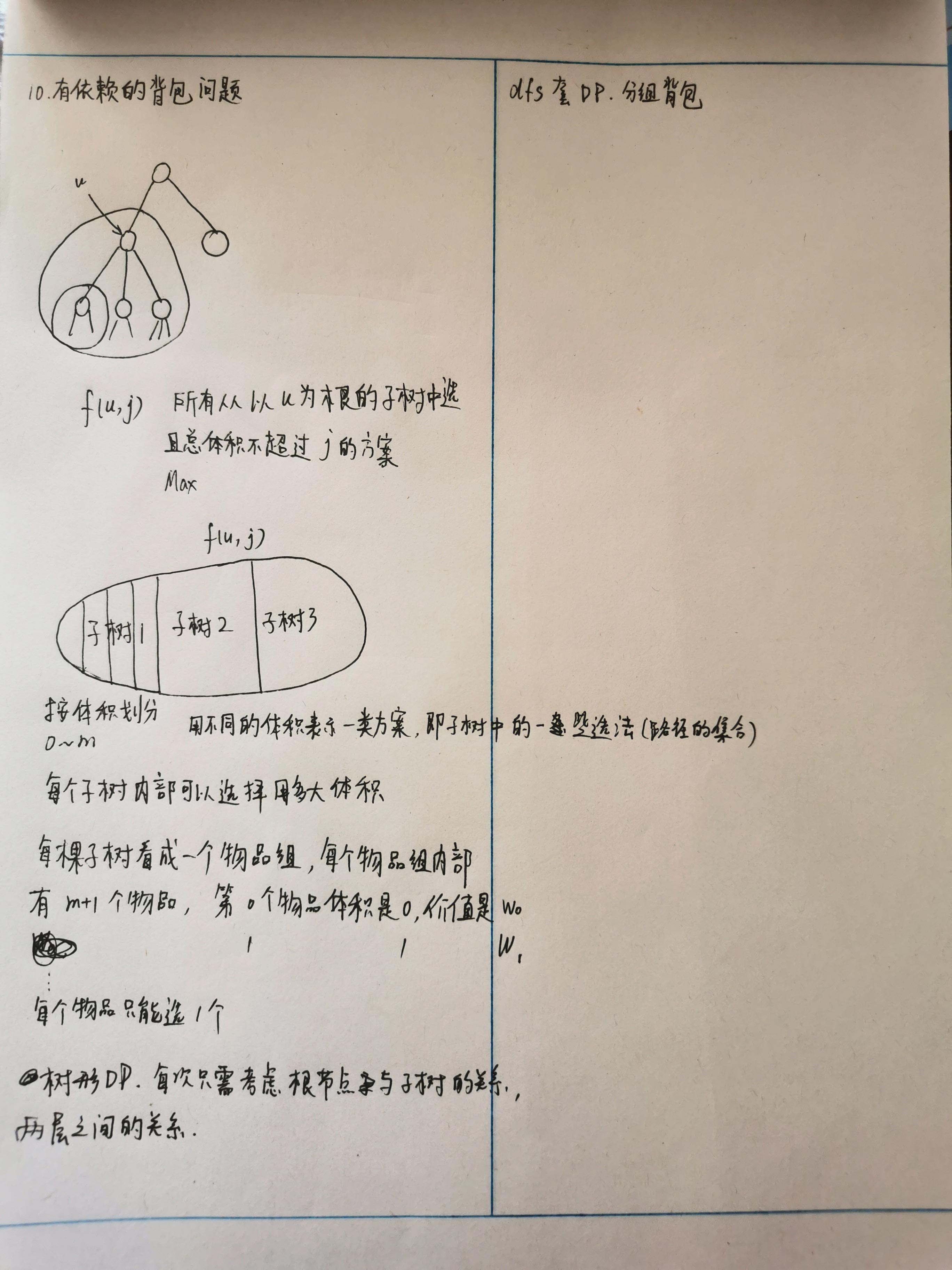
10. 有依赖的背包问题

树形 DP，DFS 套分组背包 DP。

f(u,j)f(u, j) 表示所有从以 u 为根的子树中选，且总体积不超过 j 的方案的最大价值。

按体积 0 ~ m 划分，用不同的体积表示一类方案，即这棵子树中的一类选法。

每棵子树看成一个物品组，每个物品组内部有 m + 1 个物品：

第 0 个物品体积是 0，价值是 f[son][0]；son 是子树的节点号
第 1 个物品体积是 1，价值是 f[son][1]；
…

物品组内只能选一个物品。物品组内的物品和题目给的物品不是一个概念，物品组内的一个物品对应在当前这棵子树中题目物品的一类选法。

每次只需要考虑根节点与子树的关系，上下两层，可以 dfs。

有依赖的背包问题 DP 分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <cstring>
#include <iostream>
using namespace std;

const int N = 110;
int v[N], w[N];
int h[N], e[N], ne[N], idx;
int f[N][N];
int n, m;

void add(int a, int b) {
  e[idx] = b;
  ne[idx] = h[a];
  h[a] = idx++;
}

void dfs(int u) {
  for (int i = h[u]; i != -1; i = ne[i]) {  // 循环物品组
    int son = e[i];
    dfs(e[i]);
    // 分组背包
    for (int j = m - v[u]; j >= 0; j--) {  // 循环体积，如果选子树，那么必须选根节点，所以要把 v[u] 的体积预留出来
      for (int k = 0; k <= j; k++) { // 循环决策，选物品组中哪个物品（不是哪个子树），每个物品对应当前考虑的子树中的一类选法
        f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
      }
    }
  }
  // 将物品 u 加进去
  for (int j = m; j >= v[u]; j--) {
    f[u][j] = f[u][j - v[u]] + w[u];
  }
  // 由于必须选 u 根节点，背包体积小于 v[u] 的情况无法装入任何物品，最大价值置为 0
  for (int j = 0; j < v[u]; j++) {
    f[u][j] = 0;
  }
}

int main() {
  cin >> n >> m;
  memset(h, -1, sizeof h);
  int root;
  for (int i = 1; i <= n; i++) {
    int p;
    cin >> v[i] >> w[i] >> p;
    if (p == -1)
      root = i;
    else
      add(p, i);
  }
  dfs(root);
  cout << f[root][m] << endl;
  return 0;
}

11. 背包问题求方案数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <cstring>
#include <iostream>
using namespace std;

const int N = 1010, mod = 1e9 + 7;
int n, m;
int f[N], g[N];

int main() {
  cin >> n >> m;
  memset(f, -0x3f, sizeof f);
  f[0] = 0;
  g[0] = 1;
  for (int i = 0; i < n; i++) {
    int v, w;
    cin >> v >> w;
    for (int j = m; j >= v; j--) {
      int maxv = max(f[j], f[j - v] + w);
      int cnt = 0;
      if (maxv == f[j]) cnt += g[j];
      if (maxv == f[j - v] + w) cnt += g[j - v];
      g[j] = cnt % mod;
      f[j] = maxv;
    }
  }
  int res = 0;
  for (int i = 0; i <= m; i++) res = max(res, f[i]);
  int cnt = 0;
  for (int i = 0; i <= m; i++) {
    if (res == f[i]) {
      cnt = (cnt + g[i]) % mod;
    }
  }
  cout << cnt << endl;
  return 0;
}

734. 能量石

面对一堆能量石，我们要决定吃那些能量石，按照什么顺序来吃，两个维度。对于顺序问题，我们可以先对所有能量石按照 SiLi\frac{S_i}{L_i} 来排序，然后在这个顺序下考虑选择那些吃能量石。

贪心证明：

对于相邻的两块能量石 ii 和 i+1i+1，先吃 ii 再吃 i+1i+1 得到的能量为 Ei+Ei+1−Si⋅Li+1E_i + E_{i+1} - S_i \cdot L_{i+1}，先吃 i+1i+1 再吃 ii 得到的能量为 Ei+1+Ei−Si+1⋅LiE_{i+1} + E_i - S_{i+1} \cdot L_{i}。所以当 Si⋅Li+1<Si+1⋅LiS_i \cdot L_{i+1} < S_{i+1} \cdot L_{i} 时，先吃 ii 再吃 i+1i+1，反之先吃 i+1i+1 再吃 ii.

整理一下，对所有能量石按照 SiLi\frac{S_i}{L_i} 排序。

接下来是一个 01 背包问题，f(i,j)f(i, j) 表示的集合：所有从前 i 块能量石中选，吃完花费时间恰好为 j 的选法。属性：获得能量的最大值。

状态转移方程：f(i,j)=max(f(i−1,j),f(i−1,j−Si)+max(0,Ei−(j−Si)⋅Li))f(i, j) = max(f(i-1,j), f(i-1, j-S_i)+max(0, E_i-(j-S_i) \cdot L_i)).

如果选择吃第 i 块能量石，此时时间已经过了 j−Sij-S_i，获取的能量为需要扣除 (j−Si)⋅Li(j-S_i) \cdot L_i，但不能为负数，所以和 0 取一个 max. 代码实现上，由于计算 f[i][j] 时也要取 max，所以后一项不写 max 也没问题，是负数的情况会在计算 max 时丢弃。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;

const int N = 10010;
int f[N];

struct Stone {
  int s, e, l;
  bool operator<(const Stone &e) const { return s * e.l < e.s * l; }
} stone[N];

int main() {
  int T;
  cin >> T;
  for (int C = 1; C <= T; C++) {
    int n;
    int m = 0;
    cin >> n;
    for (int i = 0; i < n; i++) {
      cin >> stone[i].s >> stone[i].e >> stone[i].l;
      m += stone[i].s;
    }
    sort(stone, stone + n);
    memset(f, -0x3f, sizeof f);
    f[0] = 0;
    for (int i = 0; i < n; i++) {
      int s = stone[i].s, e = stone[i].e, l = stone[i].l;
      for (int j = m; j >= s; j--) {
        f[j] = max(f[j], f[j - s] + e - (j - s) * l);
      }
    }
    int res = 0;
    for (int i = 0; i <= m; i++) res = max(res, f[i]);
    printf("Case #%d: %d\n", C, res);
  }
  return 0;
}